1引(yin)言
   渦輪(lun)流量計(ji) 所謂脈(mo)動流是(shi)指流體(ti)在測量(liang)區域的(de)流速是(shi)時間的(de)函數(但(dan)👈在❓一個(ge)足夠長(zhang)的時間(jian)段内有(you)一個恒(heng)定的平(ping)均值，脈(mo)動流的(de)存在會(hui)導緻 流(liu)量計 出(chu)現計量(liang)誤差(甚(shen)至不能(neng)正常工(gong)作，如何(he)校正或(huo)減少㊙️脈(mo)✔️動對流(liu)量測量(liang)特性的(de)影響(是(shi)流量測(ce)量中比(bi)㊙️較重要(yao)的🌈課題(ti)⚽。 |
2、脈動對(dui)渦輪流(liu)量計流(liu)量測量(liang)的影響(xiang)
2.1誤差方(fang)程及其(qi)計算
   應(ying)用機翼(yi)理論來(lai)分析作(zuo)用在渦(wo)輪轉子(zi)上的驅(qu)動力矩(ju)和阻力(li)矩(可得(de)到其運(yun)動方程(cheng)：

   式中 ，J爲(wei)葉片轉(zhuan)動慣量(liang)θ爲葉片(pian)與軸線(xian)之間的(de)夾角💋r爲(wei)渦輪葉(ye)片的平(ping)均半徑(jing)，A爲管道(dao)流道面(mian)積，ρ爲流(liu)體密度(du)，ω爲渦🐆輪(lun)的💃🏻旋轉(zhuan)，角速度(du)Q爲通過(guo)管道的(de)流量。
若(ruo)把脈動(dong)流表示(shi)爲，經分(fen)析整理(li)，可得出(chu)渦輪旋(xuan)轉加速(su)度與脈(mo)動流各(ge)參數的(de)關系：

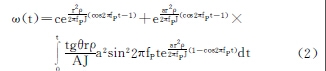
其中，c爲(wei)穩态時(shi)的ω值。此(ci)時其顯(xian)示誤差(cha)可用下(xia)式表示(shi)：E=ω/C--1
對特定(ding)的渦輪(lun)流量計(ji)和不同(tong)的脈動(dong)流,可編(bian)程計算(suan)出(2)式‼️在(zai)♈脈動周(zhou)期内各(ge)離散點(dian)所對應(ying)的ω(t)，據此(ci)可計算(suan)出渦輪(lun)流🎯量計(ji)顯示🏃‍♀️誤(wu)差E，并畫(hua)出相應(ying)曲線。
2.2結(jie)果與分(fen)析
   經過(guo)計算分(fen)析，發現(xian)導緻渦(wo)輪流量(liang)計産生(sheng)誤差的(de)主要🔞因(yin)素是🥵脈(mo)動流的(de)振幅和(he)頻率，通(tong)過對多(duo)幅圖形(xing)的比較(jiao)🏃🏻，發現有(you)如下規(gui)律：

1. 從曲(qu)線分布(bu)的象限(xian)來看，脈(mo)動流導(dao)緻渦輪(lun)流量計(ji)出現一(yi)個正誤(wu)差。當流(liu)體存在(zai)脈動時(shi)，在加速(su)流體中(zhong)，葉片的(de)轉動🧑🏽‍🤝‍🧑🏻慣(guan)量🔞能引(yin)起轉子(zi)速度變(bian)慢，落後(hou)于定常(chang)流時的(de)轉💜速；在(zai)減🌍速流(liu)體🐅中，葉(ye)片的轉(zhuan)動慣量(liang)能導緻(zhi)轉子速(su)度加快(kuai)，超過定(ding)常流時(shi)的轉速(su)。由于加(jia)速時的(de)影響比(bi)減速時(shi)的影響(xiang)小得多(duo)，因此：脈(mo)動流存(cun)在時流(liu)量計顯(xian)示的平(ping)均流速(su)遠大于(yu)平均流(liu)🙇🏻量，出現(xian)正誤差(cha)(此💋誤差(cha)有時最(zui)大可達(da)50%。
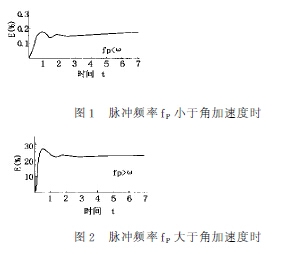
2. 當脈動(dong)頻率fpx小(xiao)于渦輪(lun)轉子的(de)角頻率(lü)ω時，流量(liang)計類似(si)輸🈲入脈(mo)沖，測量(liang)結果接(jie)近真值(zhi)，脈動流(liu)所引起(qi)的誤差(cha)很小。當(dang)脈動頻(pin)🧑🏾‍🤝‍🧑🏼率fp大于(yu)渦輪轉(zhuan)子的角(jiao)頻率ω時(shi)，響應失(shi)真，會引(yin)起較大(da)誤差，且(qie)随着頻(pin)率的增(zeng)大，誤差(cha)随着增(zeng)大，最終(zhong)趨于穩(wen)定（如圖(tu)1，圖2）
   
   
   
   
3. 當脈(mo)動頻率(lü)大于渦(wo)輪轉子(zi)的角加(jia)速度時(shi),頻率脈(mo)動振幅(fu)的變化(hua)能引起(qi)渦輪流(liu)量計的(de)測量誤(wu)差産生(sheng)大🍉的改(gai)變,此誤(wu)差⛱️随着(zhe)脈動振(zhen)幅的增(zeng)大而升(sheng)高,最大(da)可達
   
   
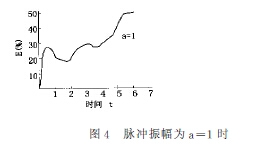
   50%,但(dan)最終趨(qu)于穩定(ding)（如圖3,圖(tu)4，a爲脈動(dong)振幅與(yu)穩态振(zhen)幅✨之比(bi)）。

結論
    從(cong)以上分(fen)析計算(suan)可知，脈(mo)動流使(shi)渦輪流(liu)量計産(chan)生一個(ge)正的🈲系(xi)統誤差(cha)，該誤差(cha)受脈動(dong)頻率和(he)振幅的(de)影響。當(dang)脈動頻(pin)率小💜于(yu)角加速(su)度時，其(qi)誤差可(ke)認爲爲(wei)零；當脈(mo)動振幅(fu)小于某(mou)一振幅(fu)值時🔴，其(qi)誤差亦(yi)可認爲(wei)不影🐉響(xiang)渦輪流(liu)☂️量計的(de)精🌈度。脈(mo)動流對(dui)渦輪流(liu)🛀🏻量計測(ce)量精确(que)度的影(ying)響🌏存在(zai)極限值(zhi)。

本文 來(lai)源于網(wang)絡,如有(you)侵權聯(lian)系删除(chu)轉載請(qing)注明出(chu)處！！