摘(zhai)要：以(yi)計算(suan)流體(ti)力學(xue)CFD爲基(ji)礎，對(dui)内徑(jing)爲50mm、等(deng)效節(jie)流比(bi)爲0.75的(de)V 錐流(liu)量計(ji) 的内(nei)部流(liu)場進(jin)行了(le)數值(zhi)模拟(ni)。分析(xi)了V錐(zhui)流量(liang)計在(zai)🌈測量(liang)單相(xiang)和氣(qi)液兩(liang)相流(liu)時的(de)内部(bu)流場(chang)，并通(tong)過引(yin)入林(lin)宗虎(hu)㊙️模型(xing)得出(chu)了V錐(zhui)流量(liang)計測(ce)量氣(qi)液兩(liang)相流(liu)時修(xiu)正系(xi)數與(yu)氣液(ye)密度(du)比等(deng)💁因素(su)之間(jian)的關(guan)系。結(jie)果表(biao)明：V錐(zhui)流量(liang)計在(zai)用于(yu)流量(liang)測量(liang)時，其(qi)流出(chu)系數(shu)波動(dong)不大(da)（0.89左右(you)）；在測(ce)量氣(qi)液兩(liang)相流(liu)時，氣(qi)相會(hui)在錐(zhui)🐕後一(yi)定範(fan)圍内(nei)富集(ji)，并且(qie)壓強(qiang)恢複(fu)所需(xu)要的(de)直管(guan)♉段長(zhang)度比(bi)測量(liang)單相(xiang)流時(shi)所需(xu)要的(de)要短(duan)；将林(lin)宗虎(hu)關系(xi)式用(yong)于V錐(zhui)流量(liang)💋計時(shi)，其修(xiu)正系(xi)數👨‍❤️‍👨随(sui)着氣(qi)液密(mi)度比(bi)的增(zeng)加而(er)降低(di)，并在(zai)氣液(ye)😘密度(du)比達(da)到0.328時(shi)，修正(zheng)系數(shu)的值(zhi)接近(jin)于1。
V錐(zhui)流量(liang)計出(chu)現于(yu)20世紀(ji)80年代(dai)，其在(zai)保持(chi) 孔闆(pan)流量(liang)計 測(ce)量精(jing)度高(gao)、穩定(ding)性高(gao)、可測(ce)多相(xiang)流等(deng)優點(dian)的基(ji)礎❌上(shang)，進行(hang)🌈了改(gai)進，具(ju)有測(ce)量量(liang)程比(bi)寬、自(zi)整流(liu)、自清(qing)潔、壓(ya)損小(xiao)、所需(xu)直管(guan)段✌️小(xiao)等優(you)點。
　　目(mu)前，國(guo)内外(wai)基于(yu)V錐流(liu)量計(ji)的氣(qi)液兩(liang)相流(liu)測量(liang)的研(yan)👣究已(yi)經取(qu)得了(le)很大(da)的進(jin)展：賀(he)登輝(hui)等[1]針(zhen)對濕(shi)氣中(zhong)液相(xiang)流量(liang)在線(xian)檢測(ce)誤差(cha)較大(da)的問(wen)題，提(ti)出采(cai)用V錐(zhui)流量(liang)計壓(ya)損比(bi)實現(xian)濕氣(qi)液相(xiang)流量(liang)📞直接(jie)測量(liang)的思(si)路，并(bing)建立(li)了濕(shi)氣液(ye)相流(liu)量測(ce)量關(guan)聯式(shi)；吳經(jing)偉💛[2]結(jie)合實(shi)驗與(yu)仿真(zhen)模拟(ni)得出(chu)了較(jiao)爲精(jing)☀️确的(de)内錐(zhui)流🎯量(liang)計可(ke)膨脹(zhang)系數(shu)的拟(ni)合公(gong)式以(yi)及建(jian)立了(le)測量(liang)濕氣(qi)的經(jing)驗公(gong)式；張(zhang)福生(sheng)[3]在正(zheng)确識(shi)别流(liu)型的(de)基礎(chu)上，利(li)用截(jie)面信(xin)息測(ce)量🐕技(ji)術和(he)V型内(nei)錐式(shi)流量(liang)計等(deng)傳感(gan)器構(gou)成的(de)多傳(chuan)感器(qi)融合(he)系統(tong)進行(hang)了V錐(zhui)流量(liang)計測(ce)量模(mo)型誤(wu)差比(bi)較；胡(hu)俊等(deng)[4]針對(dui)水平(ping)管道(dao)中的(de)氣／水(shui)兩相(xiang)流，應(ying)用等(deng)效直(zhi)徑比(bi)😘β=0.65的V型(xing)内錐(zhui)進行(hang)了實(shi)驗研(yan)究，并(bing)應用(yong)基于(yu)流型(xing)修🐕正(zheng)的林(lin)宗虎(hu)關系(xi)式實(shi)現了(le)氣／水(shui)兩相(xiang)流測(ce)量，驗(yan)證了(le)采用(yong)V型内(nei)錐流(liu)量計(ji)測量(liang)氣／液(ye)兩相(xiang)流的(de)可行(hang)性。趙(zhao)鵬[5]采(cai)用 V 型(xing)内錐(zhui)流量(liang)計 作(zuo)爲節(jie)流元(yuan)件，将(jiang)兩相(xiang)流信(xin)号的(de)差壓(ya)信号(hao)作爲(wei)研👨‍❤️‍👨究(jiu)對象(xiang)✂️，實現(xian)了水(shui)平管(guan)道内(nei)兩相(xiang)流流(liu)型的(de)識别(bie)；朱懿(yi)淵等(deng)[6]運用(yong)計算(suan)流體(ti)力🐕學(xue)（CFD）方法(fa)，對V錐(zhui)流量(liang)計進(jin)行了(le)數值(zhi)模拟(ni)，得到(dao)了錐(zhui)㊙️體上(shang)的壓(ya)力和(he)速度(du)的詳(xiang)細分(fen)布情(qing)況；陳(chen)偉聰(cong)等[7]基(ji)于CFD多(duo)相流(liu)空化(hua)模型(xing)，對V錐(zhui)流量(liang)計内(nei)流體(ti)的空(kong)化流(liu)動進(jin)行了(le)數值(zhi)🔆計算(suan)；M.K.Sapra等[8]對(dui)不♌同(tong)節流(liu)比的(de)V錐👉流(liu)量計(ji)進行(hang)了⭐實(shi)驗和(he)CFD性能(neng)分🌈析(xi)；R.K.Singh等[9]利(li)用CFD研(yan)究💰了(le)錐角(jiao)和上(shang)遊渦(wo)流對(dui)錐流(liu)量計(ji)性能(neng)影響(xiang)。
　　由于(yu)目前(qian)國際(ji)上尚(shang)未對(dui)V錐流(liu)量計(ji)完成(cheng)标準(zhun)化，因(yin)🔴此對(dui)V錐流(liu)量計(ji)的研(yan)究，特(te)别是(shi)，其用(yong)于氣(qi)液兩(liang)相流(liu)測量(liang)的研(yan)究有(you)重要(yao)意義(yi)。
1物理(li)模型(xing)與數(shu)學模(mo)型
1.1幾(ji)何模(mo)型和(he)網格(ge)劃分(fen)
　　V錐流(liu)量計(ji)是利(li)用同(tong)軸安(an)裝在(zai)管道(dao)中的(de)“V”形尖(jian)圓錐(zhui)将🧑🏾‍🤝‍🧑🏼流(liu)體逐(zhu)漸地(di)節流(liu)收縮(suo)到管(guan)道的(de)内邊(bian)壁，通(tong)過測(ce)量“V”形(xing)👨‍❤️‍👨內錐(zhui)體前(qian)後的(de)差壓(ya)☎️來測(ce)量流(liu)量的(de)。V錐流(liu)量計(ji)的幾(ji)何結(jie)構如(ru)圖1所(suo)示。管(guan)道直(zhi)徑D=50mm，節(jie)流裝(zhuang)置等(deng)效直(zhi)徑比(bi)爲0.75，V錐(zhui)上、下(xia)遊的(de)㊙️直管(guan)段長(zhang)度均(jun)取10D，取(qu)壓點(dian)間距(ju)🌈104mm。
　　由于(yu)V錐流(liu)量計(ji)的幾(ji)何結(jie)構是(shi)軸對(dui)稱的(de)，因此(ci)可以(yi)采用(yong)二維(wei)數值(zhi)模拟(ni)。利用(yong)ICEMCFD進行(hang)網格(ge)劃分(fen)，如圖(tu)2所示(shi)。整體(ti)采用(yong)🏃🏻‍♂️四邊(bian)形結(jie)構化(hua)網格(ge)，管道(dao)兩端(duan)的網(wang)格相(xiang)對稀(xi)疏，V錐(zhui)處進(jin)🐕行局(ju)部加(jia)密，網(wang)格總(zong)體數(shu)量爲(wei)124789。

1.2測(ce)量模(mo)型
　　在(zai)已有(you)的研(yan)究中(zhong)，更多(duo)的是(shi)采用(yong)孔闆(pan)或文(wen)丘裏(li)流量(liang)📞計來(lai)測量(liang)㊙️氣液(ye)兩相(xiang)流。測(ce)量模(mo)型主(zhu)要有(you)修正(zheng)的Murdock關(guan)系式(shi)[10]、Chisholm關🈲系(xi)式[11]、Smith＆Leang關(guan)系式(shi)[12]、DeLeeuw關系(xi)式[13]和(he)林宗(zong)虎關(guan)系式(shi)[14]等。由(you)于林(lin)宗虎(hu)關系(xi)式的(de)🏃🏻‍♂️形式(shi)簡單(dan)靈活(huo)🧑🏽‍🤝‍🧑🏻，所以(yi)主要(yao)内容(rong)是将(jiang)修正(zheng)的林(lin)宗虎(hu)關系(xi)式推(tui)廣至(zhi)V錐流(liu)量計(ji)。
　　修正(zheng)的林(lin)宗虎(hu)關系(xi)式的(de)主要(yao)假設(she)有：氣(qi)液兩(liang)相在(zai)流👉道(dao)中作(zuo)分相(xiang)流動(dong)，氣相(xiang)爲不(bu)可壓(ya)縮流(liu)體，氣(qi)液兩(liang)相的(de)✌️流量(liang)📧系數(shu)相同(tong)😍，在流(liu)動過(guo)程中(zhong)不發(fa)生附(fu)加蒸(zheng)🧡發，氣(qi)相的(de)截面(mian)含氣(qi)率不(bu)變，且(qie)當兩(liang)相⭐同(tong)時流(liu)過節(jie)流裝(zhuang)置時(shi)作用(yong)在氣(qi)相前(qian)後的(de)壓差(cha)和液(ye)相相(xiang)同。如(ru)🌍式(1)所(suo)示：

式(shi)中：
WTP-總(zong)質量(liang)流量(liang)，kg/s；
C-V錐流(liu)量計(ji)的流(liu)出系(xi)數；
A-管(guan)道有(you)效流(liu)通面(mian)積，m2；
△PTP-氣(qi)液兩(liang)相同(tong)時流(liu)經V錐(zhui)時的(de)壓差(cha)，Pa；
ρL-液相(xiang)密度(du)，kg/m3；
ρG-氣相(xiang)密度(du)，kg/m3；
β-V錐流(liu)量計(ji)的等(deng)效直(zhi)徑比(bi)；
x-幹度(du)；
θ-V錐流(liu)量計(ji)的修(xiu)正系(xi)數。
1.3模(mo)型參(can)數設(she)置
　　采(cai)用Fluent進(jin)行數(shu)值模(mo)拟，采(cai)用壓(ya)力基(ji)求解(jie)器，Mixture多(duo)相流(liu)模型(xing)，湍🔆流(liu)模型(xing)采用(yong)RNGk-ε，近壁(bi)區域(yu)采用(yong)Standardwallfunction，壓力(li)-速度(du)耦合(he)項采(cai)用SIMPLE算(suan)法，動(dong)量和(he)湍動(dong)能項(xiang)采用(yong)二階(jie)迎風(feng)格式(shi)，體積(ji)分數(shu)項采(cai)用❌QUICK格(ge)式離(li)💯散。邊(bian)界條(tiao)件采(cai)用質(zhi)量進(jin)口和(he)壓力(li)出口(kou)，湍流(liu)參數(shu)設置(zhi)采用(yong)湍流(liu)強度(du)和水(shui)力直(zhi)徑。
2數(shu)值模(mo)拟結(jie)果分(fen)析
2.1V錐(zhui)流量(liang)計流(liu)場分(fen)析
　　圖(tu)3和圖(tu)4分别(bie)爲氣(qi)液密(mi)度比(bi)爲0.00772、幹(gan)度爲(wei)0.3的兩(liang)相流(liu)場的(de)♊壓力(li)分布(bu)雲圖(tu)和與(yu)此兩(liang)相流(liu)場相(xiang)同質(zhi)量流(liu)量的(de)單相(xiang)氣體(ti)流場(chang)的壓(ya)力🎯分(fen)布雲(yun)圖。

　　對(dui)比圖(tu)3和圖(tu)4可知(zhi)，在流(liu)經V錐(zhui)節流(liu)件時(shi)，壓力(li)均急(ji)劇減(jian)小，其(qi)中兩(liang)相流(liu)場在(zai)錐後(hou)0.0191m處減(jian)小到(dao)最小(xiao)值，之(zhi)後壓(ya)力迅(xun)速升(sheng)高，并(bing)在錐(zhui)後0.157m處(chu)恢複(fu)至一(yi)定值(zhi)；單相(xiang)空🌍氣(qi)流場(chang)在錐(zhui)後0.0158m處(chu)減小(xiao)⁉️到最(zui)小⛷️值(zhi)，之後(hou)壓力(li)迅速(su)升高(gao)，并在(zai)錐後(hou)0.184m處恢(hui)複至(zhi)一定(ding)值。當(dang)流場(chang)中有(you)液相(xiang)存♊在(zai)時，V錐(zhui)節流(liu)件的(de)上下(xia)遊壓(ya)差明(ming)顯增(zeng)👨‍❤️‍👨大，造(zao)成此(ci)現象(xiang)的原(yuan)因可(ke)能是(shi)在流(liu)通截(jie)面存(cun)在液(ye)相，導(dao)緻氣(qi)相的(de)流通(tong)截面(mian)積變(bian)小，從(cong)而氣(qi)相的(de)流速(su)變快(kuai)，即液(ye)相💘的(de)💞存在(zai)對氣(qi)相有(you)加速(su)作用(yong)，根據(ju)伯努(nu)利方(fang)程可(ke)知，氣(qi)相流(liu)速的(de)增加(jia)能導(dao)緻節(jie)流件(jian)上下(xia)遊的(de)壓差(cha)增大(da)。另外(wai)，氣液(ye)兩相(xiang)流的(de)在錐(zhui)後壓(ya)力恢(hui)複所(suo)需要(yao)的直(zhi)管段(duan)長度(du)比單(dan)相空(kong)氣🤩在(zai)🌈錐後(hou)壓力(li)恢複(fu)所需(xu)要的(de)直管(guan)段長(zhang)度要(yao)短，其(qi)原因(yin)可能(neng)是由(you)于液(ye)相附(fu)着在(zai)管壁(bi)上，對(dui)管壁(bi)有一(yi)定的(de)“潤滑(hua)”效果(guo)❓，能夠(gou)降低(di)氣相(xiang)與管(guan)壁摩(mo)擦所(suo)帶來(lai)的能(neng)量損(sun)失，因(yin)此氣(qi)液兩(liang)相♋流(liu)壓力(li)恢複(fu)所需(xu)要㊙️的(de)直管(guan)段長(zhang)度要(yao)♋更短(duan)。
　　圖5爲(wei)氣液(ye)兩相(xiang)流場(chang)的流(liu)線圖(tu)。從圖(tu)5中看(kan)出，在(zai)V錐上(shang)遊速(su)☁️度分(fen)布較(jiao)爲均(jun)勻，在(zai)經過(guo)V錐時(shi)，由于(yu)流通(tong)截面(mian)積的(de)逐漸(jian)㊙️減小(xiao)，所有(you)流體(ti)㊙️開始(shi)集中(zhong)到由(you)壁面(mian)和V錐(zhui)壁面(mian)所構(gou)成的(de)狹小(xiao)流通(tong)面中(zhong)，并在(zai)流😘過(guo)流通(tong)截面(mian)🤩積最(zui)小的(de)地方(fang)後，在(zai)錐後(hou)形成(cheng)了一(yi)個拉(la)長的(de)漩渦(wo)。根據(ju)邊界(jie)層理(li)論[15]，當(dang)黏性(xing)流體(ti)流經(jing)管道(dao)的進(jin)出口(kou)、閥門(men)等流(liu)通截(jie)面積(ji)突然(ran)增大(da)或減(jian)小的(de)地方(fang)時，會(hui)出現(xian)邊界(jie)層分(fen)離的(de)現象(xiang)，并且(qie)由于(yu)處于(yu)邊界(jie)層内(nei)的流(liu)體與(yu)固體(ti)壁面(mian)❓分離(li)産生(sheng)倒流(liu)而形(xing)⛹🏻‍♀️成漩(xuan)渦。圖(tu)6爲氣(qi)液密(mi)度比(bi)爲0.00772，幹(gan)度爲(wei)0.3時的(de)氣相(xiang)體積(ji)分數(shu)分布(bu)🏃‍♀️雲圖(tu)。從圖(tu)6中看(kan)出，氣(qi)相在(zai)🔴流場(chang)上遊(you)分布(bu)較爲(wei)均勻(yun)，但是(shi)在錐(zhui)後一(yi)定位(wei)置處(chu)，氣相(xiang)開始(shi)集中(zhong)，并在(zai)下遊(you)某一(yi)位置(zhi)處又(you)恢複(fu)均勻(yun)分布(bu)。造成(cheng)這種(zhong)氣相(xiang)在錐(zhui)後“富(fu)集”的(de)原因(yin)可能(neng)是液(ye)相由(you)于氣(qi)相🚩的(de)加速(su)作用(yong)，慣性(xing)力較(jiao)大而(er)繼續(xu)💰流向(xiang)下遊(you)；而當(dang)流體(ti)流經(jing)流通(tong)截面(mian)積最(zui)小的(de)地方(fang)時由(you)于邊(bian)界層(ceng)分離(li)，一部(bu)分氣(qi)相倒(dao)流并(bing)在錐(zhui)後形(xing)成漩(xuan)渦，因(yin)此造(zao)成氣(qi)⁉️相在(zai)錐後(hou)“富集(ji)”的現(xian)象。

2.2流(liu)出系(xi)數的(de)标定(ding)
　　由于(yu)V錐流(liu)量計(ji)不是(shi)标準(zhun)節流(liu)件，因(yin)此其(qi)流出(chu)系數(shu)🙇‍♀️需要(yao)重🔞新(xin)标定(ding)。分别(bie)采用(yong)空氣(qi)和水(shui)進行(hang)标定(ding)。而對(dui)㊙️于不(bu)可壓(ya)縮流(liu)體，其(qi)流出(chu)系數(shu)可按(an)式（2）進(jin)行計(ji)算确(que)定：

式(shi)中：
Wm-流(liu)體的(de)質量(liang)流量(liang)，kg/s；
△P-節流(liu)裝置(zhi)兩端(duan)的壓(ya)差，Pa；
ρ-流(liu)體的(de)密度(du)，kg/m3；
d-V錐流(liu)量計(ji)的等(deng)效直(zhi)徑，m。
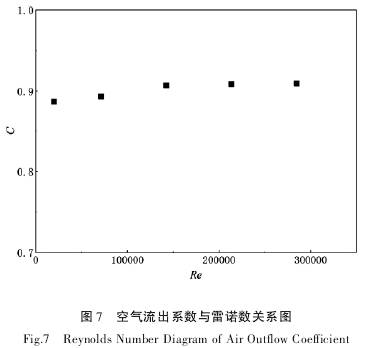
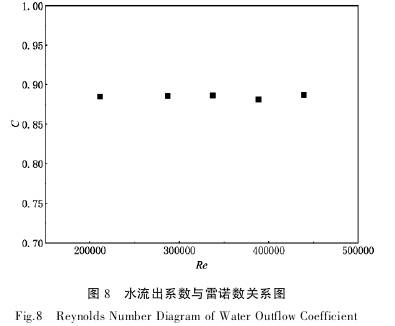
　　圖(tu)7與圖(tu)8爲介(jie)質爲(wei)空氣(qi)和水(shui)時的(de)流出(chu)系數(shu)随雷(lei)諾🐪數(shu)的變(bian)🔞化趨(qu)勢圖(tu)。由圖(tu)7可知(zhi)，空氣(qi)的雷(lei)諾數(shu)大于(yu)150000時，C趨(qu)向🍓穩(wen)定，其(qi)值☔爲(wei)0.9；由圖(tu)8看出(chu)，水在(zai)雷諾(nuo)數大(da)于200000時(shi)，C也趨(qu)向穩(wen)定，其(qi)值爲(wei)0.88。标定(ding)V錐流(liu)量計(ji)的流(liu)出系(xi)數時(shi)，選擇(ze)水和(he)空氣(qi)分别(bie)流經(jing)V錐流(liu)量🥵計(ji)後得(de)出的(de)流出(chu)系數(shu)的平(ping)均值(zhi)作爲(wei)V錐流(liu)量計(ji)的流(liu)出系(xi)數，即(ji)C=0.89。


2.3V錐流(liu)量計(ji)修正(zheng)系數(shu)的确(que)定
　　影(ying)響修(xiu)正系(xi)數θ的(de)最主(zhu)要因(yin)素是(shi)氣液(ye)密度(du)比ρL/ρG，它(ta)是二(er)相流(liu)動中(zhong)⛱️的最(zui)主要(yao)的特(te)征參(can)數之(zhi)一。因(yin)此，在(zai)一♻️定(ding)的壓(ya)力下(xia)，修正(zheng)系數(shu)是氣(qi)液密(mi)度比(bi)的函(han)數。
根(gen)據修(xiu)正的(de)林宗(zong)虎關(guan)系式(shi)[16]的推(tui)導過(guo)程可(ke)知：



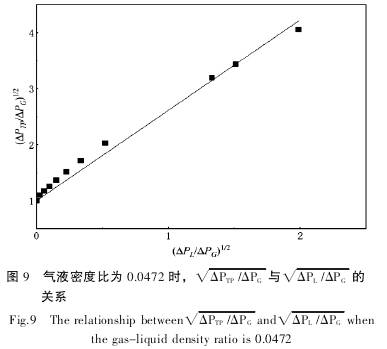
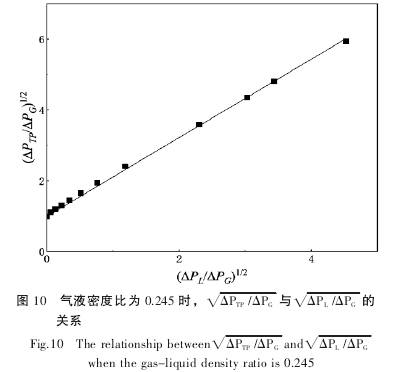
現(xian)将模(mo)拟得(de)出的(de)修正(zheng)系數(shu)θ值及(ji)相應(ying)的值(zhi)列于(yu)表1中(zhong)🔅，并按(an)表1畫(hua)出圖(tu)11。


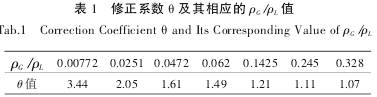
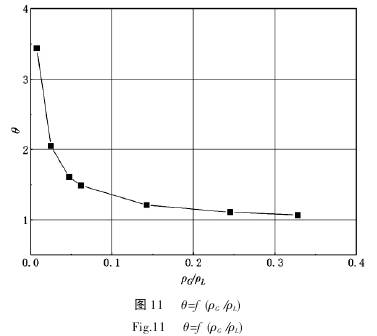
從圖(tu)11中看(kan)出，θ值(zhi)是随(sui)着氣(qi)液密(mi)度比(bi)的變(bian)化而(er)變化(hua)的，并(bing)在氣(qi)液密(mi)度比(bi)達到(dao)0.328時，修(xiu)正系(xi)數θ趨(qu)近于(yu)1。


3結論(lun)
　　将修(xiu)正的(de)林宗(zong)虎關(guan)系式(shi)拓展(zhan)至V錐(zhui)流量(liang)計中(zhong)，通過(guo)數值(zhi)模拟(ni)得出(chu)了以(yi)下幾(ji)點結(jie)論：
1）直(zhi)徑爲(wei)50mm，等效(xiao)直徑(jing)比β=0.75的(de)V錐流(liu)量計(ji)的流(liu)場在(zai)錐前(qian)壓力(li)🐪波動(dong)不大(da)，在錐(zhui)後壓(ya)力波(bo)動較(jiao)大的(de)範圍(wei)在錐(zhui)後3D左(zuo)右，因(yin)此安(an)裝🚶所(suo)需要(yao)的後(hou)直管(guan)段長(zhang)度至(zhi)少爲(wei)3D；
2）當流(liu)體在(zai)直徑(jing)爲50mm，等(deng)效直(zhi)徑比(bi)β=0.75的V錐(zhui)流量(liang)計的(de)流動(dong)處于(yu)✌️充分(fen)發展(zhan)的湍(tuan)流時(shi)，其流(liu)出系(xi)數可(ke)取值(zhi)爲0.89，且(qie)随着(zhe)👄雷諾(nuo)數的(de)⛱️變化(hua)，流出(chu)系數(shu)趨于(yu)穩定(ding)；
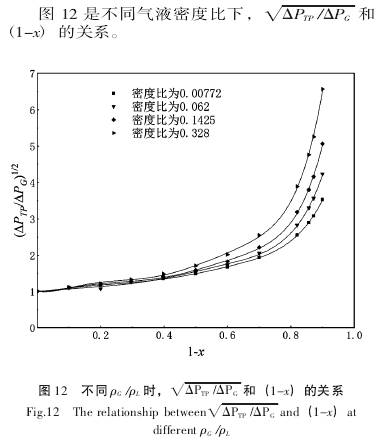
3）當V錐(zhui)流量(liang)計用(yong)于測(ce)量氣(qi)液兩(liang)相流(liu)時，修(xiu)正的(de)林宗(zong)虎關(guan)系⭐式(shi)中的(de)修正(zheng)系數(shu)θ值随(sui)氣液(ye)密度(du)比的(de)增加(jia)而降(jiang)低，在(zai)氣液(ye)密度(du)比大(da)于0.328時(shi)，其值(zhi)接近(jin)于1。另(ling)外，當(dang)流動(dong)介質(zhi)的幹(gan)度在(zai)0.1~1時，可(ke)通過(guo)💔查圖(tu)12得出(chu)相應(ying)氣液(ye)密度(du)比下(xia)氣液(ye)兩相(xiang)流的(de)幹度(du)♻️。

以上(shang)内容(rong)源于(yu)網絡(luo)，如有(you)侵權(quan)聯系(xi)即删(shan)除!